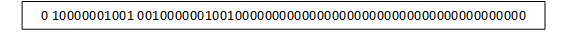`213.3`

213 -> ‘11010101’

0.3 -> ?

0.3 -> ‘01 0011 0011 0011 ….‘

Decimal number to fixed-point binary precision

From the above information 213.3 can be represented as follows :

In Fixed point the numbers are represented with a fixed number of digits after and sometimes before the decimal point eg fixed<11,3> denotes an 11-bit fixed point number of which 3 right most bits are fractional. eg real bit pattern number 11010101.010 from the example above.

How to represent this decimal number in IEEE 754 32-bit (single) floating-point notation?

In floating-point single (32-bits) or double (64-bits) precision, the number is represented with a mantissa and an exponent. The placement of the decimal point can float relative to the significant digits of the number.

Decimal number to floating-point single (32-bits) binary precision

For a 32-bit floating-point notation, need to express it in the form :

1 sign bit, 8 exponent bits, 23 fraction bits

Shift the fixed-point binary representation 7 times to the left to represent the number as a scientific notation using mantissa (affects accuracy) & exponent (affects range) :

In 8-bit exponent the largest integer we can store is 2^8-1 = 255

Exponents we want also negative to represent very small numbers. Instead of using 2’s complement IEEE decided to bias the exponent.

Exponent bias (Expbias) = 2^(K-1) – 1

Since 8 exponent bits, K=8 . ExpBias = 2^7 – 1 = 127

The number here 213.3 is positive we add to the bias a value of 7 (E’=ExpBias+E=127 + 7=134dec) [134dec == ‘10000110’ binary]

Note: If sign bit = 0 (positive number) E’=E+ExpBias else E’=E-ExpBias

The number in IEEE754 32-bit floating point notation becomes :

How to represent this decimal number in IEEE 754 64-bit (double) floating-point notation?

Decimal number to floating-point single (64-bits) binary precision

For a 64-bit floating-point notation, need to express it in the form :

1 sign bit, 11 exponent bits, 52 fraction bits

Since 11 exponent bits, K=11 . Exponent bias = 2^10 – 1 = 1023

Bias for double-precision format is 1023

The number 213.3 is positive we add to the bias a value of 7 (E’=ExpBias+E=1023+7=1030dec) [1030 dec == ‘10000000110’ binary]

The number in IEEE754 64-bit floating point notation becomes :

`1153.125`

1153 -> ‘10010000001’

.125 -> 0.001 (0*0.5 + 0*0.25 + 1*0.125)

Decimal number to fixed-point binary precision

From the above information 1153.125 can be represented as follows :

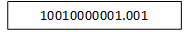
The above fixed point binary precision denotes a 14-bit fixed point number of which 3 right most bits are fractional